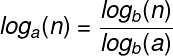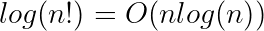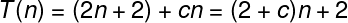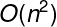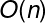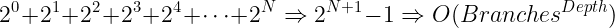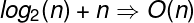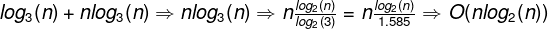All You Need to Know About “Algorithms Complexity Analysis” and Big O

What is the time complexity of this Algorithm? How much space will it take?

In the coming 10 min, you will learn how to answer those typical interview questions**.** Also, you will learn how to design better algorithms by comparing their run time and space.

So, here comes the expected question,

How do we know if algorithm A is better than algorithm B?

One important factor that determines the “goodness” of an algorithm is the amount of time it takes to solve a given problem. If algorithm A takes less time to solve the same problem than does algorithm B, then algorithm A is considered better.

Another important factor in comparing two algorithms is the amount of memory required to solve a given problem. The algorithm that requires less memory is considered better.

Now, we will focus on time analysis as it's the most tricky one.

Common Asymptotic Notations

1. Big-θ (Big-Theta) notation (Describes the ‘average' case scenario)

Big θ notation

Big-θ

When we say that particular running time is θ(n) it means that when N gets big enough, running time will be at least k1n* and at most k2n* for some constant k1 & k2.
For small values of n, we do not care how running time compares to k1n and k2n.
We are not restricted to N we can use any function as n² or n log(n) or any function.

2. Big-O (Big Ooh) notation (Describes the ‘worst-case scenario)

Big-O

We use the big-O notation for asymptotic upper bounds since it bounds the growth of the running time from above for large enough input sizes.
Big O notation is only giving the maximum running time without caring about the minimum.
Recall that we write f(n) = O(g(n)) to express the fact that f(n) grows no faster than g(n).

3. Big-Ω (Big Omega) notation (describes the ‘best' case scenario)

Big Ω

We use the big-Ω notation for asymptotic lower bounds.
We use it to say that it will take at least this amount of time to run this algorithm. After all, you know that it won't be faster than those runtimes.

In algorithm analysis, we tend to focus on the worst-case time and space complexity. This is why it is most common to see Big O being used when talking about an algorithm's time or space complexity.

Best Case, Worst Case, and Expected Case

We can describe our runtime for an algorithm in three different ways.

Let's look at this from the perspective of quick sort.

Quick sort picks a random element as a “pivot” and then swaps values in the array such that the elements less than pivot appear before elements greater than the pivot. This gives a “partial sort:'Then it recursively sorts the left and right sides using a similar process.

Best Case: If all elements are equal, then quick sort will, on average, just traverse through the array once. This is O(N).
Worst Case: What if we get really unlucky and the pivot is repeatedly the biggest element in the array? This will degenerate to an O(N²) runtime (Actually, this can easily happen. If the pivot is chosen to be the first element in the subarray and the array is sorted in reverse order, we'll have this situation.) In this case, our recursion doesn't divide the array in half and recurs on each half. It just shrinks the subarray by one element.
Expected Case: Usually, though, these wonderful or terrible situations won't happen. Sure, sometimes the pivot will be very low or very high, but it won't happen over and over again. We can expect a runtime of O(N log N).

We rarely ever discuss best case time complexity, because it's not a very useful concept. After all, we could take essentially any algorithm, special case some input, and then get an O(1) time in the best case.

For many-probably most algorithms, the worst case and the expected case are the same. Sometimes they're different, though, and we need to describe both of the runtimes.

What is the relationship between best/worst/expected case and big 0/theta/omega?

It's easy for candidates to muddle these concepts (probably because both have some concepts of “higher”, “lower” and “exactly right”), but there is no particular relationship between the concepts.

Best, worst, and expected cases describe the big O (or big theta) time for particular inputs or scenarios.

Big 0, big omega, and big theta describe the upper, lower, and tight bounds for the runtime.

A Comparison of Some Common Functions

It is easy to work with simple polynomials in N, but when the time complexity involves other types of functions like log(n), you may find it hard to identify the “highest order term”. The following table lists some commonly encountered functions in ascending order of rate of growth. Any function can be given as Big O of any other function that appears later in this table.

Order or growth

╔═════════════════╦══════════════╗ ║ Function ║ Name ║ ╠═════════════════╬══════════════╣ ║ 1. Any constant ║ Constant ║ ║ 2. log n ║ Logarithmic ║ ║ 3. log^2 n ║ Log-square ║ ║ 4. √n ║ Root-n ║ ║ 5. N ║ linear ║ ║ 6. n * log n ║ Linearithmic ║ ║ 7. n ^ 2 ║ Quadratic ║ ║ 8. n ^ 3 ║ Cubic ║ ║ 9. n ^ 4 ║ Quartic ║ ║ 10. 2 ^ n ║ Exponential ║ ║ 11. e ^ n ║ Exponential ║ ║ 12. n! ║ n-Factorial ║ ╚═════════════════╩══════════════╝

The following graph visually shows some of the functions from the above table.

Order of growth

Quick math revision and hints that are useful in complexity analysis:

General Tips

Every time a list or array gets iterated over c * length times, it is most likely in O(n) time.
When you see a problem where the number of elements in the problem space gets halved each time, it will most probably be in the O(log n) runtime.
Whenever you have a single nested loop, the problem is most likely in quadratic time O(n²).

List of Important Complexities

1. Simple for-loop with an increment of size 1

Running time Complexity Analysis

Dropping the leading constants → n + 2

Dropping lower order terms → O(n)

2. For-loop with increments of size k

Running time Complexity Analysis

3. Simple nested For-loop

Running time Complexity Analysis

4. Nested For-loop with dependent variables

Running time Complexity Analysis

5. Nested For-loop With Index Modification

Running time Complexity Analysis

6. Loops with log(n) time complexity

Running time Complexity Analysis

7. Recursive Call

Running time Complexity Analysis

The tree will have depth N. Each node (i.e., function call) has two children. Therefore, each level will have twice as many calls as the one above it.

The space complexity of this algorithm will be O(N). Although we have 0(2N) nodes in the tree total, only O(N) exists at any given time. Therefore, we would only need to have O(N) memory available.

Now let's see some examples in java to make sure we totally understand it

1. Big O of a Nested Loop with Addition

Running time Complexity Analysis

O(N²)

2. Big O of a Nested Loop with Subtraction

Running time Complexity Analysis

O(N²)

3. Big O of Nested Loop with Multiplication

Running time Complexity Analysis

4. Nested Loop with Multiplication (Basic)

Running time Complexity Analysis

5. Nested Loop with Multiplication (Intermediate)

Running time Complexity Analysis

7. Nested Loop with Multiplication (Pro)

Running time Complexity Analysis

O(n)

8. Recursive Call (Tricky)

This is just a straight recursion from n to n -1 to n -2 down to 1.

It will take O(n) time.

9. Permutation of a string (Tricky)

This is a (very!) tricky one. We can think about this by looking at how many times permutation gets called and how long each call takes. We'll aim for getting as tight of an upper bound as possible.

How many times does permutation get called in its base case?

If we were to generate a permutation, then we would need to pick characters for each “slot:' Suppose we had 7 characters in the string. In the first slot, we have 7 choices. Once we pick the letter there, we have 6 choices for the next slot. (Note that this is 6 choices for each of the 7 choices earlier.) Then 5 choices for the next slot, and so on.

Therefore, the total number of options is 7 * 6 * 5 * 4 * 3 * 2 * 1, which is also expressed as 7! (7 factorial).

This tells us that there are n! permutations. Therefore, permutation is called n! times in its base case (when a prefix is a full permutation).

How many times does permutation get called before its base case?

But, of course, we also need to consider how many times lines 9 through 12 are hit. Picture a large call tree representing all the calls. There are n! leaves, as shown above. Each leaf is attached to a path of length n. Therefore, we know there will be no more than n * n ! nodes (function calls) in this tree.

How long does each function call take?

Executing line 9 takes 0(n) time since each character needs to be printed.

Line 12 and line 13 will also take O n) time combined, due to the string concatenation. Observe that the sum of the lengths of rem, prefix, and str.charAt(i) will always be n.

Each node in our call tree, therefore, corresponds to 0(n) work.

What is the total runtime?

Since we are calling permutation 0( n * n! ) times (as an upper bound), and each one takes 0( n) time, the total runtime will not exceed O ( n² * n! ).

Through more complex mathematics, we can derive a tighter runtime equation (though not necessarily a nice closed-form expression). This would almost certainly be beyond the scope of any normal interview.

Common Data Structure Operations

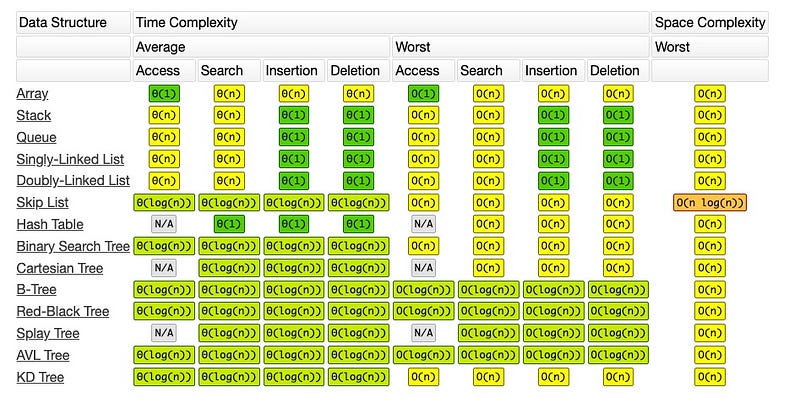
source - https://www.bigocheatsheet.com/

Array Sorting Algorithms

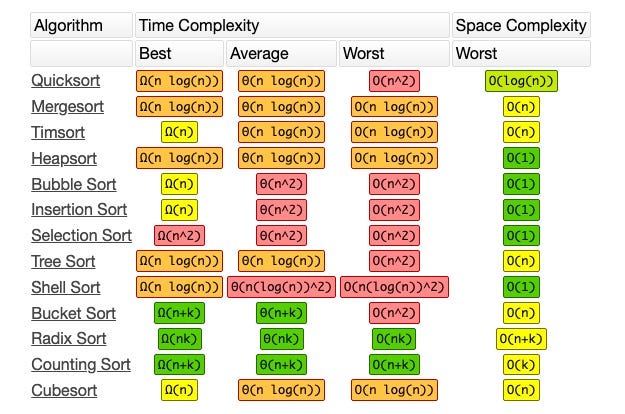
source - https://www.bigocheatsheet.com/

All You Need to Know About “Algorithms Complexity Analysis” and Big O